Preface

GAMES101是GAMES (Graphics And Mixed Environment Seminar）系列公益课程的第一部，由UCSB的助理教授闫令琪授课，该课程专注于图形学基本原理的分析与解释。本文内容为Transformation, Rasterization笔记。

Introduction

Covered Topics

• Rasterization
• Curves and Meshes
• Ray Tracing
• Animation / Simulation

References

Fundamentals Of Computer Graphics 3th Edition

---

Transformation

图形学中 Transformation 的核心问题是找到一个变换矩阵 $ M $ ，使得空间中任意一个Vetcor可以利用$M$ 进行缩放、反转、切边、旋转和平移。其中平移变换的引入需要利用齐次坐标表示$M$的仿射变换，因此，在三维向量空间中$M$应为一个4x4的矩阵。 Transformation的所有内容将基于齐次坐标构建的变换矩阵。Transformation中一个重要假设是任何复合变换都可以依次分解为各个独立变换，复合变换中，优先平移，其次线性变换。

点和向量的表示

Point = $(x,y,z,1)^\intercal$ or $(wx,wy,wz,w)^\intercal$ subject to $w>0$

Vector = $(x,y,z,0)^\intercal$（$w=0$实际上保护了Vector的平移不变性）

Scale

$$M = \left[ \begin{matrix} S_x & 0 & 0 & 0\\ 0 & S_y & 0 & 0\\ 0 & 0 & S_z & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$$

Reflection

• 以x-axis为例， y-axis, z-axis 同理。

$$M = \left[ \begin{matrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$$

Rotation

• Default
  • (0, 0, 0)为原圆心
  • 逆时针
• 由于Rotation的输入为角度$\theta$，其变换矩阵的逆刚好等于转置，满足正交矩阵性质。该性质简化了视图变换$M$的推导。

以沿x-axis旋转为例， y-axis, z-axis 同理。

$$\left[ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & \cos\theta & -\sin\theta & 0\\ 0 & \sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$$

• Rotation也满足Transformation复合叠加的假设

  $$R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)$$

• Rodrigues’ rotation formula

  罗德里格旋转公式是表达三维空间的另一种形式，其输入不再是三个轴上的旋转角度，而是选择一个单位向量 $n$ 作为旋转轴，以及 $\alpha$ 作为绕该单位向量旋转角度，公式如下：

  

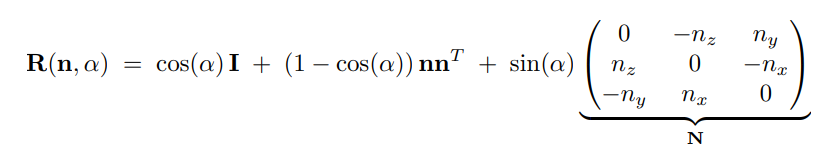
View Transform

问题描述

一个3D空间向2D投影的过程包括三步：

1. model transform
2. view transform
3. projection transform

对于View Transform， 我们定义空间中的一个相机为 $(e,g,t)$，分别代表相机的Position, Look-at Direction, Up Direction（该向量定义正交于$g$）。View Transform的目标是找到一个变换矩阵$M_{view} = R_{view}T_{view}$，使得相机的Position回到原点，Look-At Direction面向$-z$， Up Direction面向$y$

这里运用了旋转矩阵作为正交矩阵的性质，矩阵的逆等于矩阵的转置，更加直观。

Projection Transform

• Orthographic Transform
• Perspective Transform

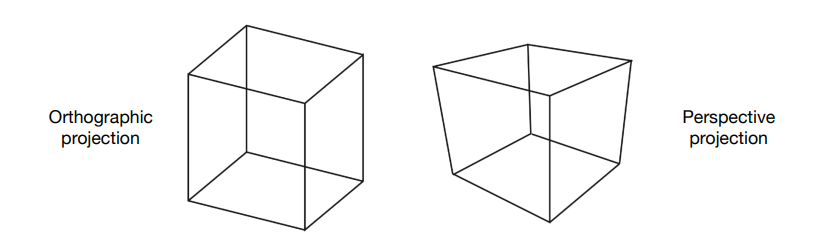
问题描述

投影变换是将3D空间信息转换为2D信息，而投影分为正交投影和透视投影，两者区别就是相机与近视屏幕的距离是否为无限。实现投影变换一个简单的思路就是去轴，例如通过移除Z轴我们就得到了X-Y平面的投影信息。但是显然这种方法是有缺陷的，大多时候我们期望投影变换后不会损失三维空间的信息。换言之，投影变换需要保留近视平面到远视平面形成的整个可视空间的信息。

因此，投影变换的目的是可视空间投影到一个以原点为中心的[1,1,1]的正则空间(canonical cube)

Orthographic Transform

Perspective Transform

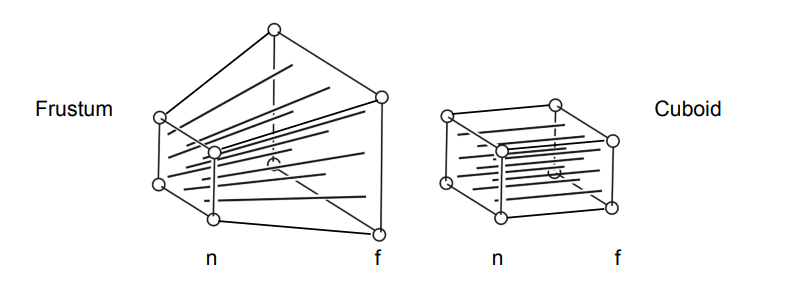
透视变换略微比正交变换复杂，因为透视相机的可视空间是一个截锥体（Frustum），这里闫老师给了一种很好理解的方式，我们先把Frustum转换为Cubiod，再使用Orthographic Transform的转换矩阵即可。而Frustum转换为Cubiod的推导也很有意思。

我们希望Frustum转换为Cubiod，首先需要使近远视平面大小一致，由于相机更接近于近视平面所以我们希望远视平面变小，就像四个手指头挤压远视平面一样。因此有如下条件

1. 相机已完成视图变换
2. 近视平面上的点恒定不变
3. 远视平面上点的Z轴信息恒定不变

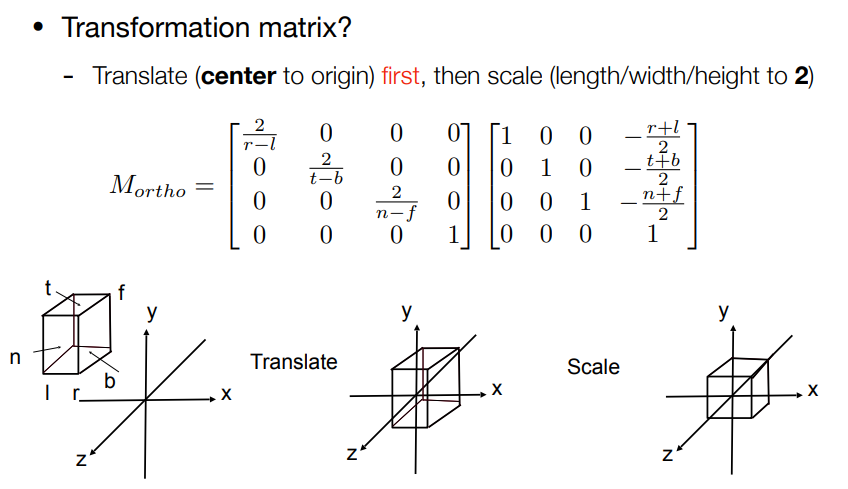
设近视平面上的点为$(x’,y’,z’)$，远视平面上的点$(x,y,z)$，分别以$-x$和$-y$的角度去观测Frustum，根据相似三角形的信息，我们可以得到

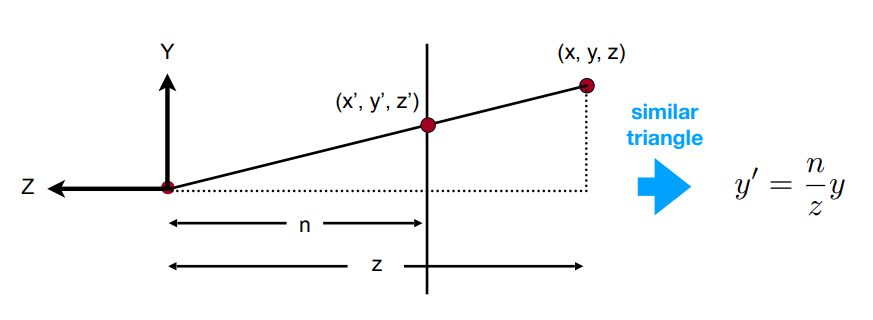
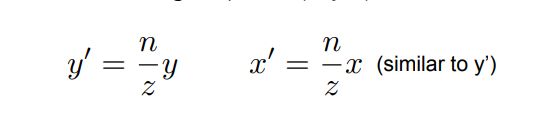
对于远视平面上的任意点，在齐次坐标下我们可以表示为

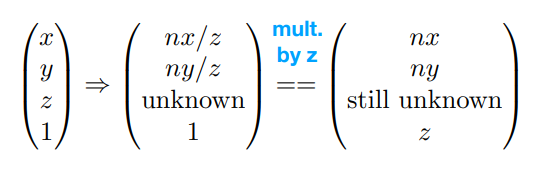
可以腿短$M_{persp\rightarrow ortho}$满足

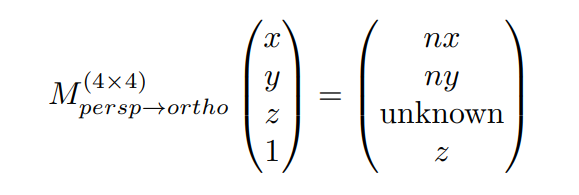
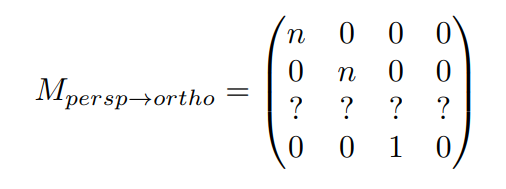
现在我们只有第三行的四个信息未知，再利用假设2可以得到

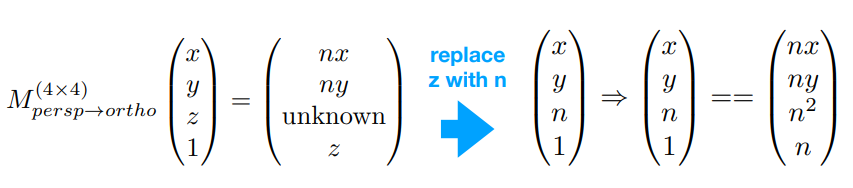
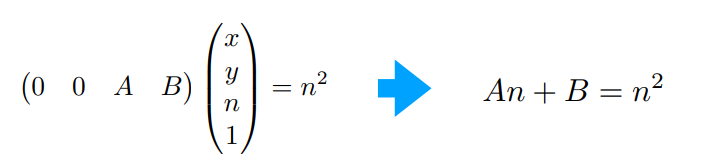
假设3可以得到

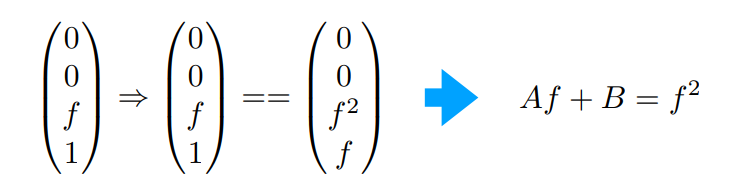
最后得出A,B

本节的思考题是在可视空间中非视平面上的点的Z轴的值是如何变化的，直观的感受我们知道Z轴的值肯定是变大的（因为远小），也可以利用矩阵计算验证，如下。

---

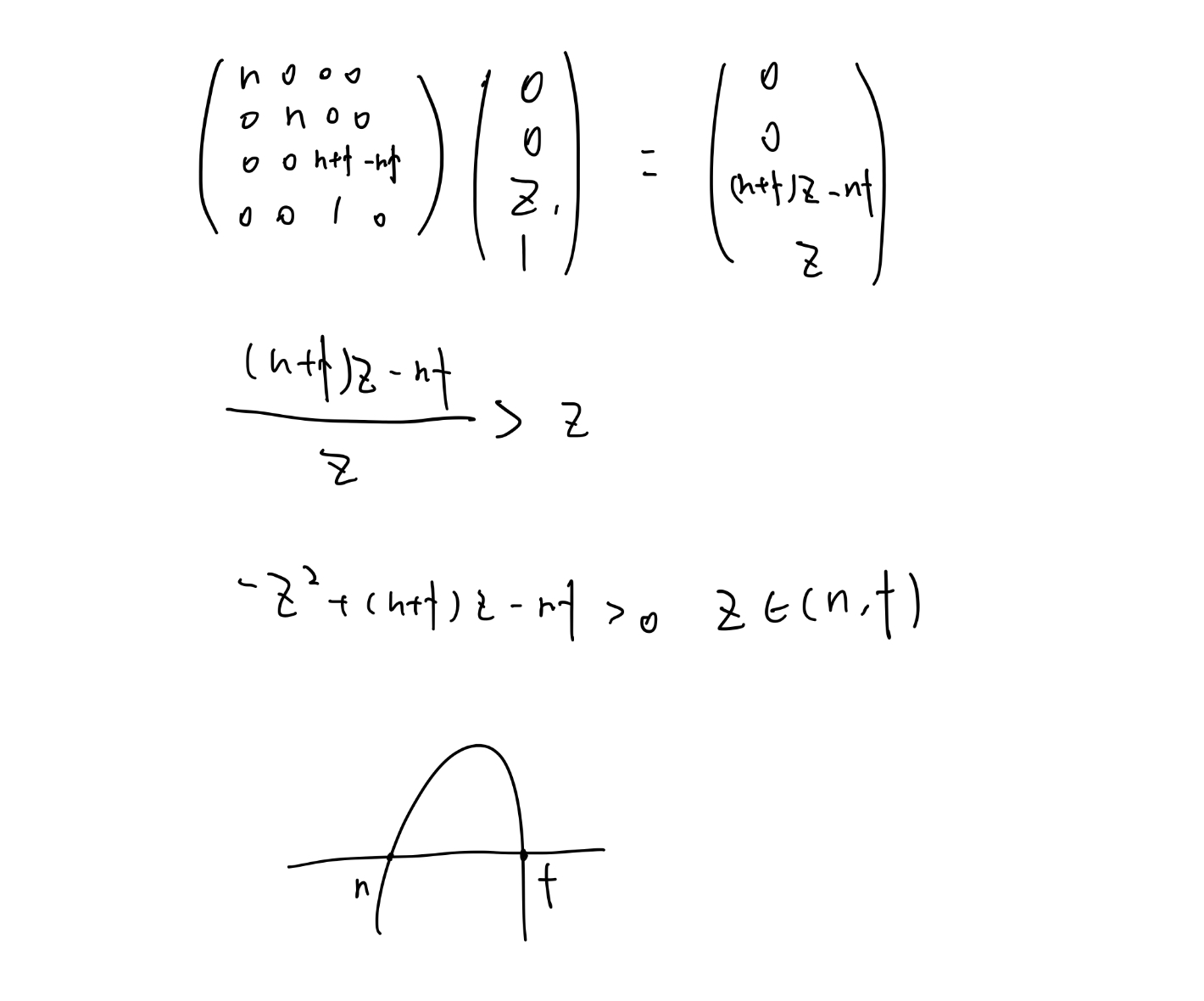
Rasterization

光栅化 (Rasterization) 是原德语的音译，实际做的就是把正则观测矩阵的信息投在屏幕上。

• Field-of-View (FOV) 相机到近平面中点的连线与其到近平面边的连线的夹角
• Aspect Ratio 横纵比 $\frac WH$

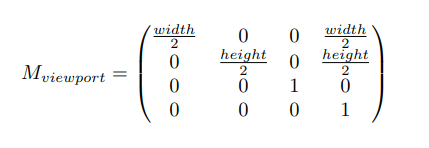
本章节定义屏幕像素是一个由RGB三色空间组成的纯色块，采用XY平面坐标系。Raster要做的是把连续的图像信息投影到离散的像素平面上，首先利用$M_{viewport}$将观测平面大小拉伸至屏幕平面大小，然后对观测空间中的三角形做离散采样。第二步具体表现为，根据每个三角形的顶点坐标定义一个操作空间，之后对操作空间每一个像素点经过$inside(tri,x,y)$函数判断其是否处在三角形内（叉乘的性质），从而判断某一像素是否需要被投影（渲染？）

这里有几个假设需要提及

1. 选择三角形的原因

   a. 最简单的多边形

   b. 三角形的三个顶点一定在一个平面，不存在凹运算

   c. 与b相似，由于三角形不存在凹运算因此内外的定义也很直接

2. 假设像素是投影的最小单元，每个像素仅有一个采样点为其中点。

3. 采样方式不一定是选取操作空间，也可以选取一个顶点作为根进行遍历。

Antialiasing

既然是采样，肯定就要涉及奈奎斯特-香农采样定理，也肯定要涉及Aliasing（信号中译为混叠，图形学译为锯齿），为了实现Antialiasing，就需要补充一些信号与系统在图形学中的解释。

我们假设图像信号是连续的波形函数，在频域中我们可以通过傅里叶级数将其分解多个不同频率的简谐函数。我们想象计算机以特定频率$F$进行采样，如果其中的某一条简谐信号的频率$F'$远大于$F$，这个频率下的信息就被错误采样了。这就导致了Aliasing。

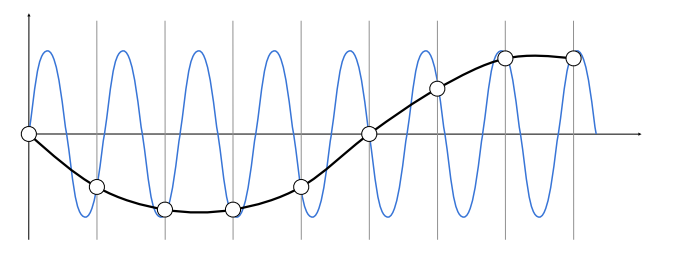
显然我们不能对单一的简谐信号操作，想要使特定频率的不被采用只需要对原信号进行滤波即可，而对于图像想好的滤波，直观上有一些比较有趣的结果。

由图可知，高频保存了边界信息，而低频保存了变化幅度较低的色块信息。解释一下频域图里的横竖亮线，这是由于图像时域信号假设中是在XY两个方向上无穷的，亮线的部分实际就是边界的突变。（这里提一下，我之前看到对抗攻击的防御中，就有通过频域识别扰动的方法，研究结果表明对抗生成的样本在频域图下不止一个高亮点，而是多个高亮点等距离分部）我们用盒形的卷积滤波器的到的图像如下。

以特定频率采样，这个过程实际上就是把图像信号的原始信息进行复制粘贴。（卷积的性质）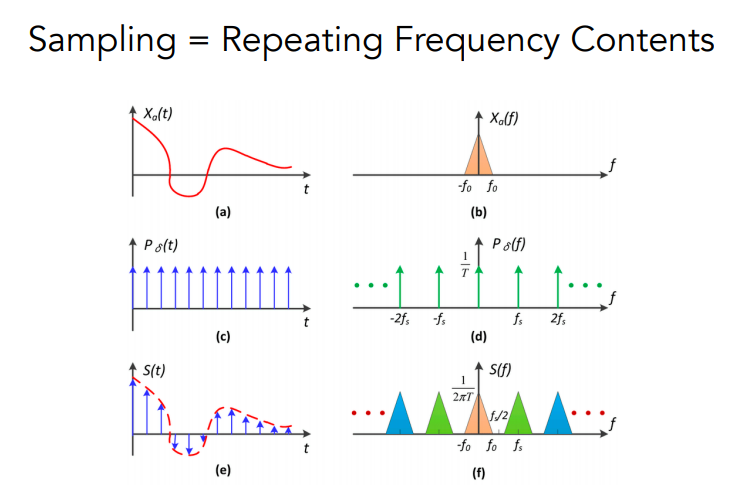

于是图像学的Aliasing和信号系统的联系了起来

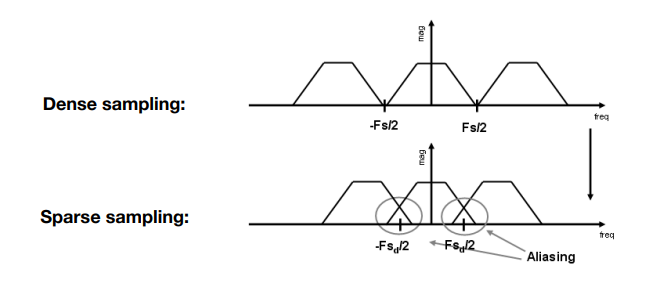
解决方法也很直接

1. 提高采样频率
2. 整个低通滤波器

然而在每个像素不止一个采样点的假设下，就能有一种更优的方案。根据每个像素中三角形内的采样点占总采样点数目的比例，我们可以动态的决定每一个像素要如何滤波，而不是对整体运用一个滤波器。这样相当于用更多的采样点换取更少的计算量。这也是MSAA的核心思路。

Antialiasing Today

这里简要介绍一下，FXAA就是拓展了MSAA的假设，即每个像素内的采样点分布不是均匀的，而会根据光栅化类型利用一些算法智能分布。TAA则是通过前一帧或前几帧的采样点设置信息来动态的设置本该帧某些特定的采样点，相当于是将计算在时间上打乱了。